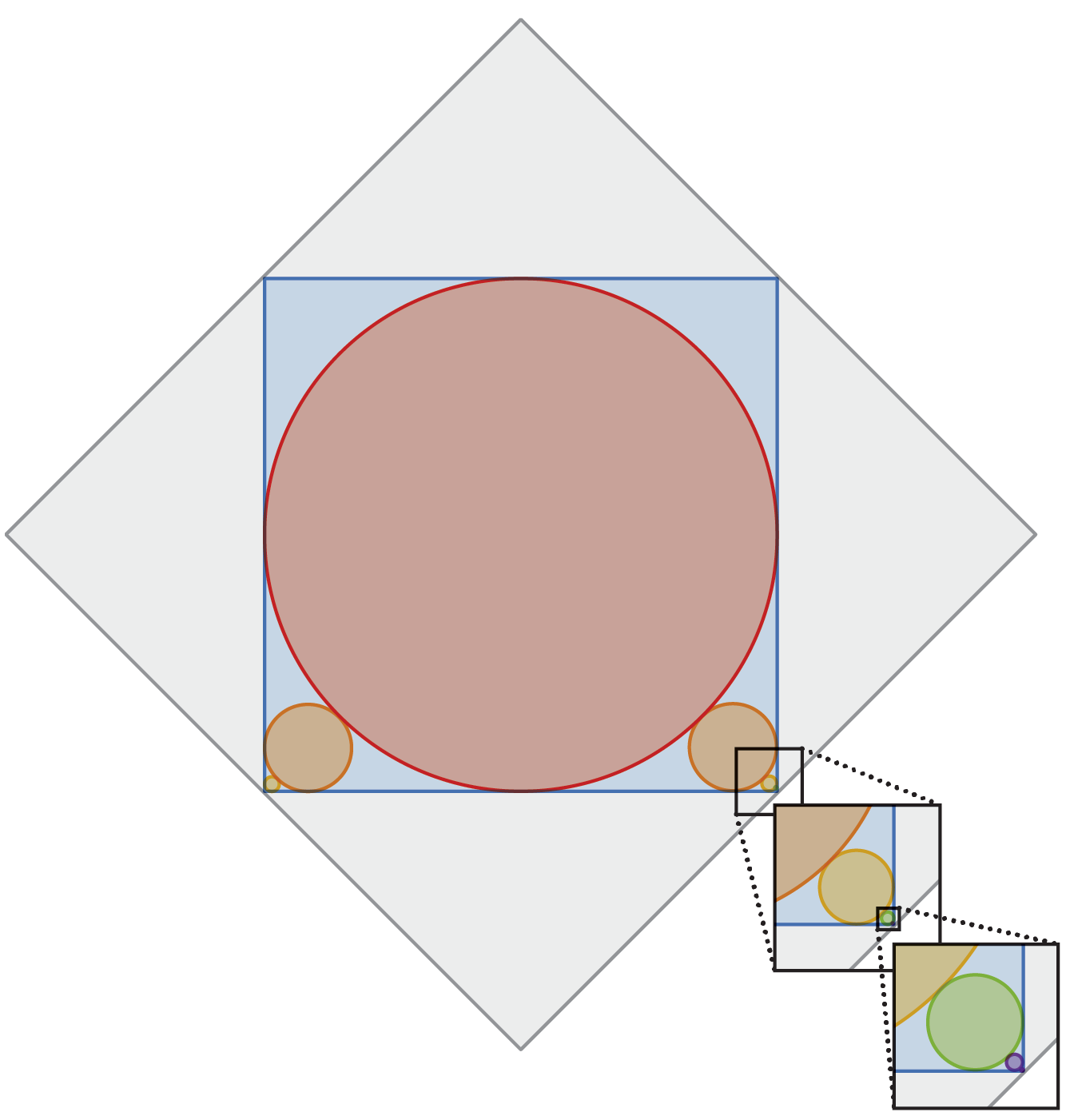
A red circle is inscribed inside a blue square. The arrangement leaves gaps in the square’s four corners, two of which are filled with smaller circles that just barely touch the big red circle and the two corner sides of the blue square. This, in turn, leaves two smaller gaps in the corners, which are filled with smaller circles, and so on, with ever smaller circles ad infinitum. The entire diagram is inscribed inside of a 1 × 1 gray square. What is the total circumference of all the circles?
The total circumference of all the circles is π. The circumference of a circle is π times its diameter. So the total circumference of many circles with diameters d1, d2, d3,… is:
πd1 + πd2 + πd3 + … = π(d1 + d2 + d3 + …)
So if we can find the sum of all the diameters, we can multiply that value by π, and we’re done. Because of the symmetry, the sizes of the circles don’t change if we move some to different corners:
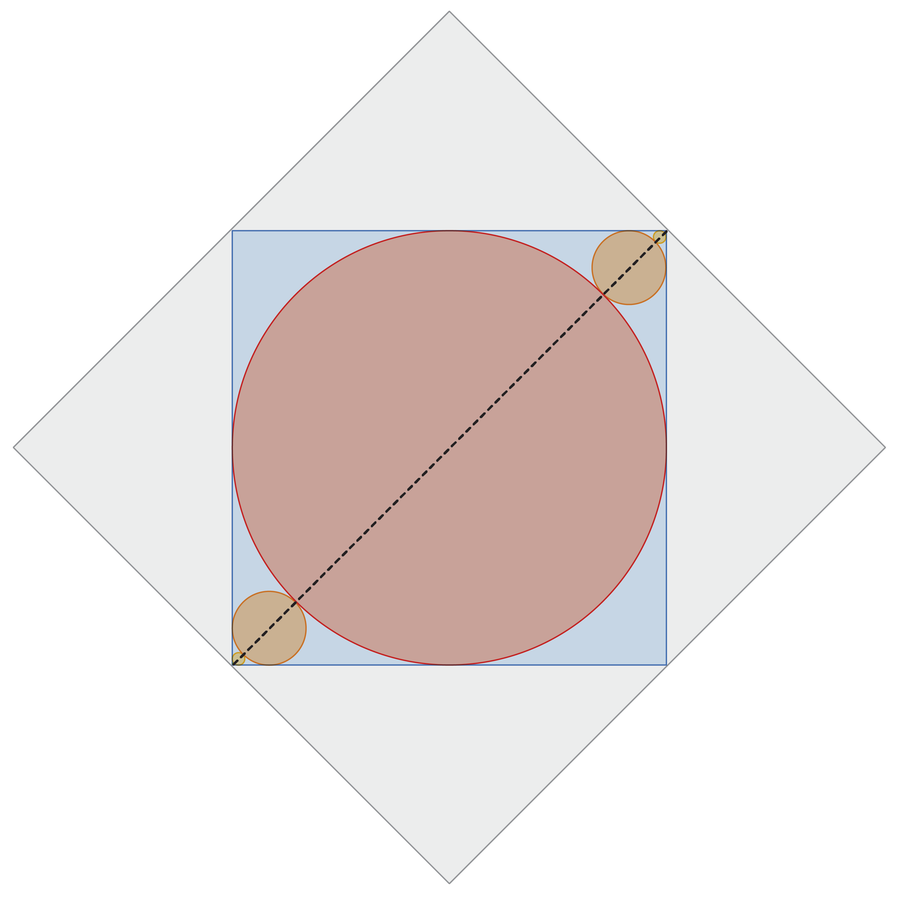
Because infinitely many circles tend toward the corners of the blue square, the sum of the circles’ diameters equals the length of the diagonal of the blue square (pictured as a dashed line). This length equals 1 because the outer gray square has side length of 1.
We’d love to hear from you! E-mail us at games@sciam.com to share your experience.